Nobel prize for causal inference: why it matters

This year's Nobel prize in economics was awarded to three brilliant economists, David Card, Joshua Angrist, and Guido Imbens for revolutionizing the way economists (and social scientists) do empirical research. Specifically, Card got it for his contributions to labor economics, and Angrist and Imbens got it for causal inference, but all three made breakthrough contributions of applying the scientific method to economics. In the field, we call it the "credibility revolution".

I am very familiar with the work of all three as I've used their papers very often while learning about causal inference, teaching it, and citing it in my own empirical research. I also had the honor of receiving comments on one of my papers (the recently published Politics of Bailouts) from Josh Angrist at a conference I co-organized. 

The way I wish to pay respects to the three of them is by explaining to you, my dear reader, why this Nobel prize in particular deconstructs that typical malevolent narrative that the economics Nobel is not really a Nobel, but rather a prize of the Swedish central bank in memory of Alfred Nobel. Why? Because this prize (like many in the past 20 years) awards empirical economists who made groundbreaking contributions in applying the true scientific method to the field. With their work, and the work of many others following in their footsteps, the field began to slowly progress from the economic orthodoxy of the pre-1990s to a much more developed field that actually has the right to start calling itself a science.

For example, the Card and Krueger (1994) paper, cited by the Nobel committee for its brilliant contribution to the field, was a state-of-the-art paper when it was published. Truly the pinnacle of the field back then. Twenty-something years later, we used it in our PhD causal inference class to pluck holes through it. We were given the data and asked to find all the errors in the paper, and explain why something like this wouldn't pass the review process today. Imagine that. Such a brilliant contribution back then wouldn't even be published today. That's how far economics (and political science, and the social sciences in general) has come today. Pure theory papers are rare. Doing some back of the envelope regressions of say, economic growth against a host of variables to see which one has a significant impact - a standard in the 1980s for example - is laughable today. Today, it is almost impossible to get an econ PhD from a decent University (say, top 400-500), without applying causal inference in your paper. Economists who still do simple regressions (or worse, elaborate their ideas without any data or proof) are by no means scientists.

Economics will never be physics (even though economists love to use complex math to mimic physics). It is more likely to follow in the footsteps of medicine and psychology (behavioral economics in particular does that), by using randomized experiments or even quasi-experiments with some random variation that enables the researcher to chose treatment and control groups. 

Why does all this matter so much? Because of the implications this new way of doing economic research will bring forward to economic policy. Thus far, the economic orthodoxy based on old theories has driven many policy conclusions. Some of the old theories were, in fact, proven correct by empirical research, but many were challenged. This has yet to be reflected in economic policy. An additional problem with economic policy is the political arena where such policies are being devised. That's why I do my empirical research in political economics, to understand how political interests shape and discourage beneficial economic policies. Sometimes it's not just about the research findings. But good research findings, based on good empirical design are still essential. It won't be long before politicians will no longer be able to dismiss them with the typical "I need a one-handed economist" argument. 

So what is causal inference and why does it matter?

If we could summarize causal inference in one cliche it would be: correlation does imply causality. 

How do you prove anything in social science? For example, that action A actually causes outcome B? For example, do better grades in school lead to higher incomes in life? If you just look at the data (below), the relationship is clearly linear and positive. But does it make it causal? No!

There can be a host of unobserved factors that might affect both grades in school and salaries later in life. Like ability. Competent individuals tend to get better grades, and have higher salaries. It wasn't the grades in that caused their salaries to be higher, it was intrinsic ability.

This is called an omitted variable bias - an issue that arises when you try to explain cause and effect without taking into consideration all the potential factors that could have affected the outcome (mostly because they were unobservable). 

Ideally we would need a counterfactual: what would the outcome be if history played out differently. What would my salary be if I didn’t go to college? Or in the absence of having metaphysical powers, we could compare individuals with different outcomes and grades, but everything else being the same.

Or we could compare twins. Genetically identical, same upbringing, same income, etc. Give one a distinction grade and the other a non-distinction, and see how they end up in life. Problem is, we cannot really interfere with people's lives just for the sake of proving a point. 

An alternative is to simply match students into comparable groups based on all of their pre-observed characteristics: gender, parental income, parental education, previous school performance, etc. Problem with this is that we can only match students based on things we can observe. We still cannot observe innate ability.

The best way to prove causality in this case, as uncovered by our Nobel winners, is to first ensure that there is random assignment into treated and controlled groups. This is essential. 

Why? Because randomization implies statistical independence. When we randomly pick who will be in the treatment and who will be in the control group, we make sure that the people in each group are statistically indistinguishable one from another. That way any difference in outcomes between the two groups should be a result of the treatment (in this case better grades), and nothing else.

Angrist did this incredibly with taking random assignmentof Vietnam war veterans (through the random draft lottery) to see how the experience of war of a randomly selected group affected their incomes later in life, compared to their peers who were lucky enough to avoid the draft.

Angrist and Krueger did it by looking at people born in firstand final quarter of a year (obvious random assignment), where those born in Q1 have worse education and income outcomes to those born in Q4.

But what if we cannot randomly assign by birth or lottery? Then we need a trick, something that generates an as-good-as random assignment; a natural threshold of some sort. Using our grades example, in the UK a distinction threshold is 70 (first honours). If you get just marginally below, 69, you get a second.Comparing someone with 75 to someone with 60 is no good; there will obviously be differences. But 70 to 69 are likely to be very similar, with one being slightly luckier. So we compare only students between 69 and 71, where those above 70 are the treatment, and those below are the control.

If there is a large enough jump, a discontinuous jump over 70 threshold where those awarded a distinction have statistically significant higher earnings than those who just barely failed to make it to the distinction grade, then we can conclude that better grades cause higher salaries. If not, if there is no jump and the relationship remains linear, then we cannot make this inference.

This design is called a regression discontinuity design (RDD). Imbens excelled at this in particular.

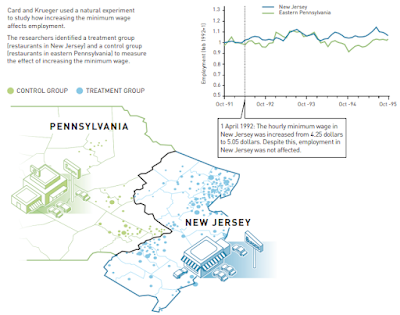
Card’s most famous contribution (with Krueger) was to use differences in differences (DID) to show how minimum wage increases impact employment. They used fast food restaurants in NJ and PA, after NJ increased the minimum wage to show that employment actually went up, not down. 

As mentioned earlier, this particular paper, state-of-the-art at the time, did not satisfy the parallel trends assumption for DID design (employment trends should have been identical in both states prior to the policy change and changed only in NJ afterwards), but Card made amends with other stellar papers on labor economics using even better research design. Like his paper on observing labor market outcomes of 125,000 Cuban immigrants coming to Florida in 1980 (you know, the plot for Brian de Palma's Scarface). 

The point here was to show how one should think about conducting natural experiments in the social sciences. It’s not about using some profound model or complex math. It’s about a change in the paradigm of drawing explicit conclusions from correlations and trends.

Finally, I want to end by paying homage to professor Alan Krueger, who tragically took his own life in 2019, and who would have surely been up there yesterday, given that two of the most important contributions made by Angrist and Card, cited by the Nobel committee, were in both cases co-authored with Krueger. To borrow one of his quotes: 

“The idea of turning economics into a true empirical science, where core theories can be rejected, is a BIG, revolutionary idea.”

Indeed it is. 

P.S. For those who want to learn more, I recommend a reading list:

• First, start with the Nobel committee's explanations. A popular version
• And a very good in-depth version
• Then, if you’re a beginner, no better place to start than Angrist and Pischke: Mastering Metrics
• Then evolve into Dunning: Natural Experiments in the Social Sciences
• Then go for: Angrist and Pischke: Mostly Harmless Econometrics (this was my bible for causal inference)
• And finally, for advanced reading, use: Gerber and Green: Field Experiments.